soalbelajar.web.id – Contoh Soal Matrik Lengkap Beserta Penjelasannya – Dalam pelajaran matematika, tentu Anda tidak asing dengan materi matriks. Materi tersebut merupakan materi yang bisa ditemukan dalam bab mata pelajaran matematika untuk jenjang pendidikan SMA.
Materi ini memang butuh ketelitian untuk mengerjakan dan memahaminya, karena itu banyak yang mencari penjelasan tambahan dan contoh soal matrik untuk dikerjakan, selain mendapatkannya dari tenaga pengajar di sekolah. Dengan terus beraltih mengerjakan, maka materi ini akan lebih mudah dipahami.
Apabila Anda memiliki masalah mengenai materi tersebut, berikut adalah penjelasan yang bisa membantu Anda memahami matriks. Tidak hanya terdapat penjelasan, tersedia contoh soal dan pembahasannya yang bisa membantu Anda.
Daftar Isi
Pengertian Dari Matriks
Sebelum masuk dalam pembahasan mengenai soal matrik, ada baiknya Anda memahami terlebih dahulu mengenai pengertian dari matriks. Dalam materi matematika, matriks merupakan kumpulan bilangan yang disusun dalam pola tertentu, yakni pola baris dan kolom. Bilangan tersebut ditata sedemikian rupa, dan ditambahkan tanda kurung untuk membedakannya dengan bilangan lain.
Bilangan yang berada di dalam tanda kurung tersebut disebut dengan elemen matriks, yang memiliki fungsi sebagai berikut:
a. Membuat penyampaian data menjadi lebih mudah, sehingga pembaca bisa memahami data dengan cepat.
b. Pengolahan data menjadi lebih mudah, sebab masing-masing data bisa dibedakan antara satu dengan yang lain.
c. Membuat pengerjaan contoh soal matriks menjadi lebih efisien dan ringkas untuk dipahami.
Anda bisa melihat penerapan mengenai matriks dalam contoh berikut ini, yakni:
Diketahui : Terdapat 3 buah mobil yang dikeluarkan oleh suatu pabrik, yakni mobil X, Y, dan Z. mobil X dijual dengan harga 125 juta rupiah, mobil Y 120 juta rupiah, sedangkan mobil Z dijual dengan harga 130 juta rupiah. Di kota Jakarta, masing-masing mobil terjual dengan jumlah 20, 25, dan 21. Sedangkan di Bandung, mobil tersebut terjual 16, 34, dan 12.
Apabila dibuat dalam bentuk matriks, maka semua data tersebut akan terbentuk sebagai berikut:
Matrik mobil yang dijual oleh perusahaan tersebut dan harganya:
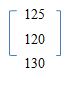
Sedangkan data penjualan mobil tersebut di masing-masing kota, dapat dijabarkan dengan urutan dan data matriks berikut:
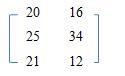
Contoh soal matriks sederhana tersebut semoga bisa membantu Anda memahami bagaimana fungsi matriks dan cara mengolahnya. Di dalam matrisk tersebut, dapat diambil kesimpulan bahwa ia terdiri dari 3 baris, dan terbagi ke dalam 2 kolom.
Perbedaan antara kolom dengan baris ini cukup mudah, kolom merupakan barisan angka yang ditata dalam bentuk vertikal ke atas menuju kebawah. Sedangkan baris merupakan barisan angka yang disusun dalam bentuk horizontal, yakni ke kiri menuju ke kanan.
Baca juga : Pembahasan Soal Vektor Dan Detailnya
Ordo Matriks dan Contoh Soal
Selain matriks secara umum, terdapat pula ordo matriks, yang masih satu bab dengan materi matriks sebelumnya. Dalam ordo matriks, masing-masing kolom diberi nama dengan simbol angka, sehingga Anda tidak kesulitan dan menulis dan membedakannya. Berikut adalah keterangan yang sering digunakan untuk membedakan kolom dan baris dalam ordo matriks:
• Untuk kolom, simbol yang digunakan adalah n. Simbol tersebut digunakan untuk mempresentasikan jummlah kolom dalam contoh soal matriks.
• Untuk baris, maka simbol yang digunakan adalah m. Simbol ini serupa dengan n, yang digunakan untuk mempresentasikan jumlah baris dalam keseluruhan data pada matriks.
Dalam ordo matriks, n dan m hanya digunakan sebagai notasi atau simbol, sehingga tidak boleh digunakan sebagai media perhitungan, baik untuk perkalian atau penjumlahan. Untuk mempermudah Anda memahami ordo matriks, berikut adalah contoh soal mengenainya.
Diketahui : Suatu pabrik memproduksi kue, yang masing-masing dinamai kue G, kue H, dan kue I. kue tersebut dijual di 4 kota yang berbeda, yakni Surabaya, Yogyakarta, Bali, dan Padang. Setiap kota memiliki tingkat penjualan yang berbeda, di Surabaya masing-masing kue terjual 40, 16, dan 21. Sedangkan di kota Yogyakarta, kue terjual sebanyak 16, 29, dan 40.
Di kota Bali, kue terjual sebanyak 16, 18, dan 17 buah, sedangkan di Padang kue tersebut terjual dengan jumlah 16, 29, dan 30. Dengan data tersebut, maka data ordo matriks dapat disusun dengan cara berikut:
Untuk membuat data ordo matriks, maka masing-masing data akan dipisahkan berdasarkan pengelompokan soa. Untuk contoh soal matriks sebelumnya, kue dibedakan berdasarkan tempat penjualannya, sehingga dapat disusun sebagai berikut:

Jangan lupa untuk menggunakan tutup kurang untuk membedakan angka tersebut dengan kumpulan angka lainnya. Dari data yang telah disusun tersebut, dapat diambil kesimpulan bahwa:
• Banyak baris dari data ordo matriks penjualan kue adalah 3 baris.
• Banyak kolom dari data ordo matriks tersebut adalah 4 kolom.
• Maka penghitungan ordo matriks yang dipakai adalah m x n = 3 x 4
Untuk melakukan penghitungan pada ordo matriks, Anda bisa menggunakan huruf capital E, yang menandakan sebagai kumpulan bilangan tersebut adalah ordo matriks. Sedangkan elemen yang ada di dalamnya disimbolisasikan dengan huruf yang lebih kecil, yakni e.
Penamaan matriks tidak boleh dilakukan sembarangan, sebab dalam contoh soal matriks, setiap elemen dan data diatur menggunakan indeks ij. Indeks tersebut akan menyatakan kolom dan baris, sehingga lebih mudah ditemukan.
Untuk memudahkan Anda dalam melakukan simbolisasi dan indeks menggunakan ordo matriks, berikut adalah cara penulisan yang benar. Untuk data ordo matriks, agar lebih ringkas, maka kita menggunakan contoh dari soal ordo matriks penjualan kue sebelumnya.
 maka penulisannnya
maka penulisannnya 
Dengan penulisan tersebut, diambil contoh Anda akan mengambil komponen e13, maka elemen matriks yang hendak Anda pakai berada di baris ke-2, yang disimbolkan dengan i=2. Sedangkan untuk kolom, e13 berada di kolom ke-3, sehingga disimbolkan dengan j=2.
Jenis Matriks
Setelah mengetahui penjelasan dan contoh soal matriks dan ordonya, Anda juga sebaiknya mengetahui bahwa matriks memiliki dua jenis, yakni matriks diagonal utama dan juga diagonal sekunder, berikut adalah penjelasan lengkapnya.
a. Matriks diagonal utama memiliki elemen yang bisa membentuk garis miring, yang membedakannya dengan matriks sekunder.
b. Matriks diagonal sekunder merupakan matriks kebalikannya, yakni ia tidak bisa memiliki diagonal miring.
Setelah mengetahui berbagai penjelasan tersebut, dapat diketahui bahwa matriks sebenarnya merupakan materi matematika yang cukup mudah untuk dipahami. Agar Anda mahir dalam penghitungan matriks dan bisa mengerjakan berbagai contoh soal matriks, maka lakukan latihan secara rutin dan pahami materinya. Semoga informasi tersebut dapat memudahkan Anda yang tengah belajar mengenai matriks dan ordonya. Terima kasih telah membaca di soalbelajar dan semoga artikel ini bisa membantu kamu.
